IEEE 754
可以参考:
https://www.zhihu.com/question/46432979/answer/221485161
https://zh.wikipedia.org/wiki/IEEE_754
https://bartaz.github.io/ieee754-visualization/
在计算机中,根据 IEEE 754 标准,所有浮点数都存储为 $\text{1.xx} \times \text{2}^{\text{yy}} \times \text{±1}$

| 类型 | 符号位 sign | 指数位 exponent | 分数位 fraction | 固定偏移值 bias |
|---|---|---|---|---|
| float | 1 | 8 | 23 | 127 |
| double | 1 | 11 | 52 | 1023 |
指数偏移值
IEEE 754 规定,设二进制浮点数的指数部分长度为 $e$,则指数偏移值的固定值是$2^{e-1}-1$。(一般,指数部分译作阶码。)因为指数部分取值实际上是 -126~127,-127 和 128 是特殊值。若指数实际值为 17,则存储为 144。
同时,采用指数的实际值加上固定的偏移值的办法表示浮点数的指数,还可以带来好处,如直接使用字典序比较浮点数大小:正数一定大于负数,无穷大于所有数,非数不能比较大小;除此之外,则可按指数域和尾数域的字典序比较。
规约
规约,指用唯一确定的浮点形式去表示一个值。
若指数部分的编码值在 $[1, 2^e-2]$ 之间(00000000001 到 11111111110),且分数部分的最高有效位是 1(000…000 到 111…111(52 位)),则这个浮点数是规约形式的。
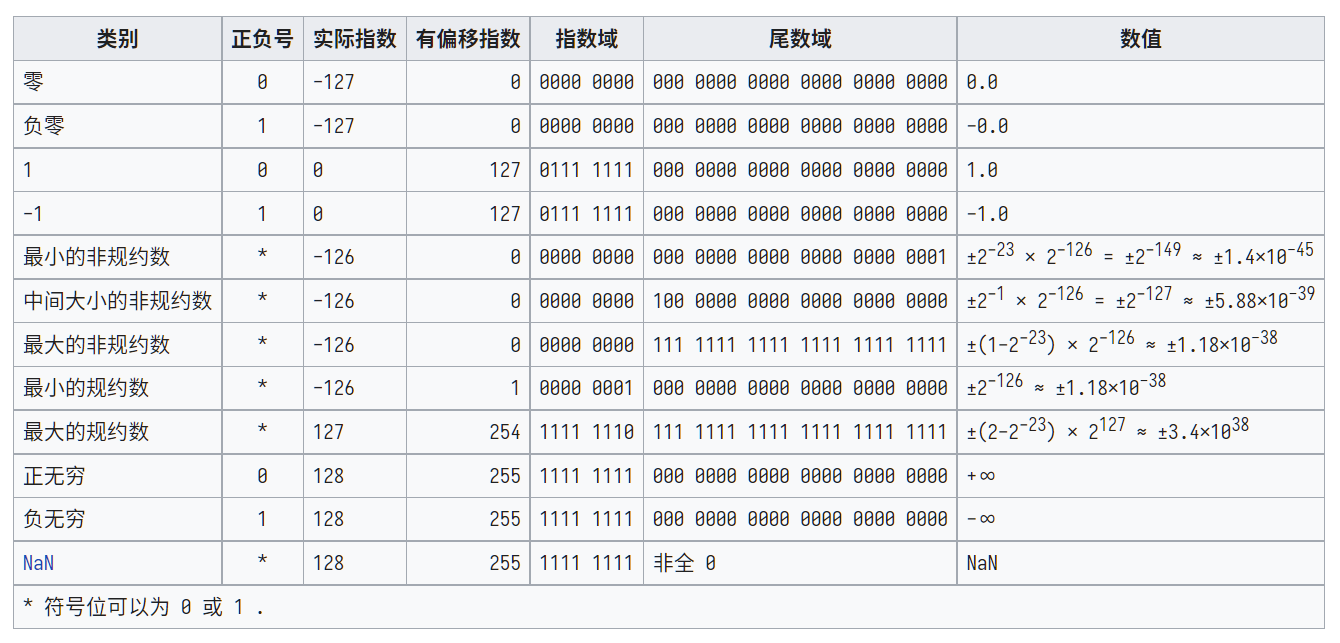
- 最小的规约数是 * - 0000 0001 - 000 0000 0000 0000 0000 0000
- 最大的规约数是 * - 1111 1110 - 111 1111 1111 1111 1111 1111
非规约形式
如果浮点数的指数部分的编码值是 0,分数部分非零,那么这个浮点数将被称为非规约形式的浮点数。
一般是某个数字相当接近零时才会使用非规约型式来表示。所有的非规约浮点数比规约浮点数更接近 0。
IEEE 754 规定,非规约形式的浮点数的指数偏移值比规约形式的浮点数的指数偏移值小 1。举例来说,对于 float 类型,规约形式偏移值是 127,而非规约的偏移值是 126。
规约浮点数的尾数大于等于 1 且小于 2,而非规约浮点数的尾数小于 1 且大于 0(规约数的尾数是有隐含 1 的,而非规约数则没有)。
- 最小的非规约数是
* - 0000 0000 - 000 0000 0000 0000 0000 0001 - 中间大小非规约数
* - 0000 0000 - 100 0000 0000 0000 0000 0000 - 最大的非规约数是
* - 0000 0000 - 111 1111 1111 1111 1111 1111
总结
| 形式 | 指数部分 | 小数部分 |
|---|---|---|
| 正负零 | 0 | 0 |
| 非规约 | 0 | 大于 0 小于 1 |
| 规约 | $[1, 2^e - 2]$ | 大于等于 1 小于 2 |
| 正负无穷 | $2^e-1$ | 0 |
| NaN | $2^e -1$ | 非零 |
精度
IEEE 规定中的小数部分实际上省略了小数点前面的 1,所以实际上 float 与 double 分别是 24、53 位。
float:$\lg{2^{23+1}} = 7.22$,7 位double:$\lg{2^{52+1}} = 15.95$,15 位
浮点截断
IEEE 754 列出了四种方法,但默认情况下,舍入到最接近,偶数优先,意思是会将结果舍入为最接近且可以表示的值,但是当存在两个数一样接近的时候,则取其中的偶数(在二进制中是以 0 结尾的)。
四舍六入五成双
- 要求保留位数的后一位如果是 4,则舍去。例如 5.214 保留两位小数为 5.21。
- 如果保留位数的后一位如果是 6,则进上去。例如 5.216 保留两位小数为 5.22。
- 如果保留位数的后一位如果是 5,而且 5 后面不再有数,要根据应看尾数 “5” 的前一位决定是舍去还是进入:如果是奇数则进入,如果是偶数则舍去。例如 5.215 保留两位小数为 5.22; 5.225 保留两位小数为 5.22。
- 如果保留位数的后一位如果是 5,而且 5 后面仍有数。例如 5.2254 保留两位小数为 5.23,也就是说如果 5 后面还有数据,则无论奇偶都要进入。
特例:
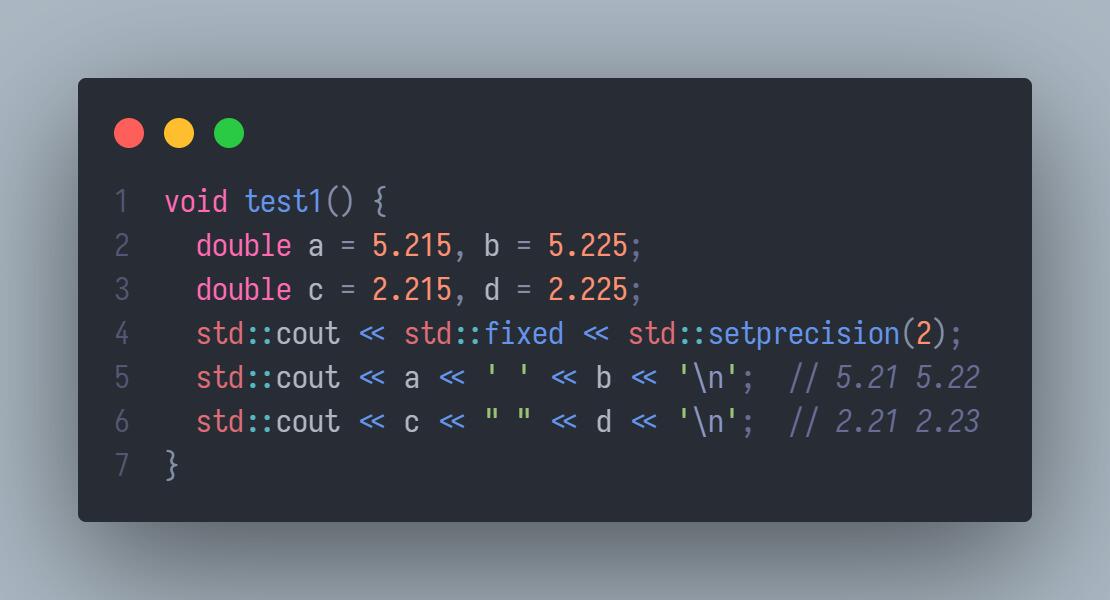
对于这一段代码,5.225 和 2.225 的保留两位小数输出结果并不相同。
这是因为,根据 IEEE 754 标准,5.225 和 2.225 分别记作 4 * 1.30625 和 2 * 1.1125,而 0.30625 和 0.1125 表示成二进制都是无限不循环小数,所以会出现浮点截断。截断后,分别是 5.22499999999999964 和 2.22500000000000008。此时再根据四舍六入五成双的规则,得到 5.22,2.23。
计算示例
例一、用 double 存储 78.375:
- 首先把 78.375 转化为二进制表示,得到 1001110.011,即 $1.001110011 \times 2^6$
- 那么,符号位是 0,小数位是 001110011 0000000…
- 6 加上固定偏移量 1023 是 1029,用二进制表示是 10000000101,这是指数位
- 所以合起来是,0 - 10000000101 - 001110011 - 00000…
例二、求 float 数据 0 10000010 01000100000000000000000 的十进制形式
- 正数
- 指数部分是 130,减去固定偏移值 127 得到实际偏移值 3
- 尾数部分是 1.010001,十进制表示为 1.265625,综合前面步骤得到 1.265625*8 = 10.125
更多示例,在 L18.pptx